ಪರಿಚಯ
ಹಿಂದಿನ ಅಧ್ಯಾಯದಲ್ಲಿ ದ್ರವಗಳು ನಿಶ್ಚಲ ಸ್ಥಿತಿಯಲ್ಲಿ ಬಳಸುವ ಬಲಗಳಿಗೆ ನಿಖರವಾದ ಗಣಿತದ ಸನ್ನಿವೇಶಗಳನ್ನು ಸುಲಭವಾಗಿ ಪಡೆಯಬಹುದು ಎಂದು ತೋರಿಸಲಾಗಿದೆ. ಏಕೆಂದರೆ ಹೈಡ್ರೋಸ್ಟಾಟಿಕ್ನಲ್ಲಿ ಸರಳ ಒತ್ತಡದ ಬಲಗಳು ಮಾತ್ರ ಒಳಗೊಂಡಿರುತ್ತವೆ. ಚಲನೆಯಲ್ಲಿರುವ ದ್ರವವನ್ನು ಪರಿಗಣಿಸಿದಾಗ, ವಿಶ್ಲೇಷಣೆಯ ಸಮಸ್ಯೆ ಒಮ್ಮೆಗೇ ಹೆಚ್ಚು ಕಷ್ಟಕರವಾಗುತ್ತದೆ. ಕಣದ ವೇಗ ಮತ್ತು ದಿಕ್ಕನ್ನು ಗಣನೆಗೆ ತೆಗೆದುಕೊಳ್ಳುವುದಲ್ಲದೆ, ಚಲಿಸುವ ದ್ರವ ಕಣಗಳ ನಡುವೆ ಮತ್ತು ಒಳಗೊಂಡಿರುವ ಗಡಿಗಳಲ್ಲಿ ಶಿಯರ್ ಅಥವಾ ಘರ್ಷಣೆಯ ಒತ್ತಡವನ್ನು ಉಂಟುಮಾಡುವ ಸ್ನಿಗ್ಧತೆಯ ಸಂಕೀರ್ಣ ಪ್ರಭಾವವೂ ಇದೆ. ದ್ರವ ದೇಹದ ವಿವಿಧ ಅಂಶಗಳ ನಡುವೆ ಸಾಧ್ಯವಿರುವ ಸಾಪೇಕ್ಷ ಚಲನೆಯು ಹರಿವಿನ ಪರಿಸ್ಥಿತಿಗಳಿಗೆ ಅನುಗುಣವಾಗಿ ಒತ್ತಡ ಮತ್ತು ಶಿಯರ್ ಒತ್ತಡವು ಒಂದು ಹಂತದಿಂದ ಇನ್ನೊಂದಕ್ಕೆ ಗಣನೀಯವಾಗಿ ಬದಲಾಗಲು ಕಾರಣವಾಗುತ್ತದೆ. ಹರಿವಿನ ವಿದ್ಯಮಾನಕ್ಕೆ ಸಂಬಂಧಿಸಿದ ಸಂಕೀರ್ಣತೆಗಳಿಂದಾಗಿ, ನಿಖರವಾದ ಗಣಿತದ ವಿಶ್ಲೇಷಣೆಯು ಕೆಲವು ಮತ್ತು ಎಂಜಿನಿಯರಿಂಗ್ ದೃಷ್ಟಿಕೋನದಿಂದ, ಕೆಲವು ಅಪ್ರಾಯೋಗಿಕ ಸಂದರ್ಭಗಳಲ್ಲಿ ಮಾತ್ರ ಸಾಧ್ಯ. ಆದ್ದರಿಂದ ಪ್ರಯೋಗದ ಮೂಲಕ ಅಥವಾ ಸೈದ್ಧಾಂತಿಕ ಪರಿಹಾರವನ್ನು ಪಡೆಯಲು ಸಾಕಷ್ಟು ಸರಳೀಕೃತ ಊಹೆಗಳನ್ನು ಮಾಡುವ ಮೂಲಕ ಹರಿವಿನ ಸಮಸ್ಯೆಗಳನ್ನು ಪರಿಹರಿಸುವುದು ಅವಶ್ಯಕ. ಯಂತ್ರಶಾಸ್ತ್ರದ ಮೂಲಭೂತ ನಿಯಮಗಳು ಯಾವಾಗಲೂ ಮಾನ್ಯವಾಗಿರುತ್ತವೆ ಮತ್ತು ಹಲವಾರು ಪ್ರಮುಖ ಸಂದರ್ಭಗಳಲ್ಲಿ ಭಾಗಶಃ ಸೈದ್ಧಾಂತಿಕ ವಿಧಾನಗಳನ್ನು ಅಳವಡಿಸಿಕೊಳ್ಳಲು ಅನುವು ಮಾಡಿಕೊಡುವುದರಿಂದ ಎರಡೂ ವಿಧಾನಗಳು ಪರಸ್ಪರ ಪ್ರತ್ಯೇಕವಾಗಿಲ್ಲ. ಸರಳೀಕೃತ ವಿಶ್ಲೇಷಣೆಯ ಪರಿಣಾಮವಾಗಿ ನಿಜವಾದ ಪರಿಸ್ಥಿತಿಗಳಿಂದ ವಿಚಲನದ ಪ್ರಮಾಣವನ್ನು ಪ್ರಾಯೋಗಿಕವಾಗಿ ಖಚಿತಪಡಿಸಿಕೊಳ್ಳುವುದು ಸಹ ಮುಖ್ಯವಾಗಿದೆ.
ದ್ರವವು ಆದರ್ಶ ಅಥವಾ ಪರಿಪೂರ್ಣವಾಗಿದೆ, ಹೀಗಾಗಿ ಸಂಕೀರ್ಣಗೊಳಿಸುವ ಸ್ನಿಗ್ಧತೆಯ ಪರಿಣಾಮಗಳನ್ನು ತೆಗೆದುಹಾಕುತ್ತದೆ ಎಂಬುದು ಅತ್ಯಂತ ಸಾಮಾನ್ಯವಾದ ಸರಳೀಕರಣ ಊಹೆಯಾಗಿದೆ. ಇದು ಸ್ಟೋಕ್ಸ್, ರೇಲೀ, ರಾಂಕಿನ್, ಕೆಲ್ವಿನ್ ಮತ್ತು ಲ್ಯಾಂಬ್ರಂತಹ ಪ್ರಖ್ಯಾತ ವಿದ್ವಾಂಸರಿಂದ ಗಮನ ಸೆಳೆದ ಅನ್ವಯಿಕ ಗಣಿತಶಾಸ್ತ್ರದ ಒಂದು ಶಾಖೆಯಾದ ಶಾಸ್ತ್ರೀಯ ಹೈಡ್ರೊಡೈನಾಮಿಕ್ಸ್ನ ಆಧಾರವಾಗಿದೆ. ಶಾಸ್ತ್ರೀಯ ಸಿದ್ಧಾಂತದಲ್ಲಿ ಗಂಭೀರವಾದ ಅಂತರ್ಗತ ಮಿತಿಗಳಿವೆ, ಆದರೆ ನೀರು ತುಲನಾತ್ಮಕವಾಗಿ ಕಡಿಮೆ ಸ್ನಿಗ್ಧತೆಯನ್ನು ಹೊಂದಿರುವುದರಿಂದ, ಅದು ಅನೇಕ ಸಂದರ್ಭಗಳಲ್ಲಿ ನಿಜವಾದ ದ್ರವವಾಗಿ ವರ್ತಿಸುತ್ತದೆ. ಈ ಕಾರಣಕ್ಕಾಗಿ, ಶಾಸ್ತ್ರೀಯ ಹೈಡ್ರೊಡೈನಾಮಿಕ್ಸ್ ಅನ್ನು ದ್ರವ ಚಲನೆಯ ಗುಣಲಕ್ಷಣಗಳ ಅಧ್ಯಯನಕ್ಕೆ ಅತ್ಯಂತ ಮೌಲ್ಯಯುತ ಹಿನ್ನೆಲೆ ಎಂದು ಪರಿಗಣಿಸಬಹುದು. ಪ್ರಸ್ತುತ ಅಧ್ಯಾಯವು ದ್ರವ ಚಲನೆಯ ಮೂಲಭೂತ ಚಲನಶಾಸ್ತ್ರಕ್ಕೆ ಸಂಬಂಧಿಸಿದೆ ಮತ್ತು ಸಿವಿಲ್ ಎಂಜಿನಿಯರಿಂಗ್ ಹೈಡ್ರಾಲಿಕ್ಸ್ನಲ್ಲಿ ಎದುರಾಗುವ ಹೆಚ್ಚು ನಿರ್ದಿಷ್ಟ ಸಮಸ್ಯೆಗಳನ್ನು ಎದುರಿಸುವ ನಂತರದ ಅಧ್ಯಾಯಗಳಿಗೆ ಮೂಲಭೂತ ಪರಿಚಯವಾಗಿ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ. ದ್ರವ ಚಲನೆಯ ಮೂರು ಪ್ರಮುಖ ಮೂಲ ಸಮೀಕರಣಗಳಾದ ನಿರಂತರತೆ, ಬರ್ನೌಲಿ ಮತ್ತು ಆವೇಗ ಸಮೀಕರಣಗಳನ್ನು ಪಡೆಯಲಾಗಿದೆ ಮತ್ತು ಅವುಗಳ ಮಹತ್ವವನ್ನು ವಿವರಿಸಲಾಗಿದೆ. ನಂತರ, ಶಾಸ್ತ್ರೀಯ ಸಿದ್ಧಾಂತದ ಮಿತಿಗಳನ್ನು ಪರಿಗಣಿಸಲಾಗುತ್ತದೆ ಮತ್ತು ನಿಜವಾದ ದ್ರವದ ನಡವಳಿಕೆಯನ್ನು ವಿವರಿಸಲಾಗುತ್ತದೆ. ಸಂಕುಚಿತಗೊಳಿಸಲಾಗದ ದ್ರವವನ್ನು ಉದ್ದಕ್ಕೂ ಊಹಿಸಲಾಗಿದೆ.
ಹರಿವಿನ ವಿಧಗಳು
ದ್ರವ ಚಲನೆಯ ವಿವಿಧ ಪ್ರಕಾರಗಳನ್ನು ಈ ಕೆಳಗಿನಂತೆ ವರ್ಗೀಕರಿಸಬಹುದು:
1. ಪ್ರಕ್ಷುಬ್ಧ ಮತ್ತು ಲ್ಯಾಮಿನಾರ್
2. ತಿರುಗುವಿಕೆ ಮತ್ತು ಕಿರಿಕಿರಿಯುಂಟುಮಾಡುವ
3. ಸ್ಥಿರ ಮತ್ತು ಅಸ್ಥಿರ
4.ಏಕರೂಪ ಮತ್ತು ಏಕರೂಪವಲ್ಲದ.
MVS ಸರಣಿಯ ಅಕ್ಷೀಯ-ಹರಿವಿನ ಪಂಪ್ಗಳು AVS ಸರಣಿಯ ಮಿಶ್ರ-ಹರಿವಿನ ಪಂಪ್ಗಳು (ಲಂಬ ಅಕ್ಷೀಯ ಹರಿವು ಮತ್ತು ಮಿಶ್ರ ಹರಿವಿನ ಸಬ್ಮರ್ಸಿಬಲ್ ಒಳಚರಂಡಿ ಪಂಪ್) ವಿದೇಶಿ ಆಧುನಿಕ ತಂತ್ರಜ್ಞಾನವನ್ನು ಅಳವಡಿಸಿಕೊಳ್ಳುವ ಮೂಲಕ ಯಶಸ್ವಿಯಾಗಿ ವಿನ್ಯಾಸಗೊಳಿಸಲಾದ ಆಧುನಿಕ ಉತ್ಪಾದನೆಗಳಾಗಿವೆ. ಹೊಸ ಪಂಪ್ಗಳ ಸಾಮರ್ಥ್ಯವು ಹಳೆಯದಕ್ಕಿಂತ 20% ದೊಡ್ಡದಾಗಿದೆ. ದಕ್ಷತೆಯು ಹಳೆಯದಕ್ಕಿಂತ 3~5% ಹೆಚ್ಚಾಗಿದೆ.

ಪ್ರಕ್ಷುಬ್ಧ ಮತ್ತು ಲ್ಯಾಮಿನಾರ್ ಹರಿವು.
ಈ ಪದಗಳು ಹರಿವಿನ ಭೌತಿಕ ಸ್ವರೂಪವನ್ನು ವಿವರಿಸುತ್ತವೆ.
ಪ್ರಕ್ಷುಬ್ಧ ಹರಿವಿನಲ್ಲಿ, ದ್ರವ ಕಣಗಳ ಪ್ರಗತಿಯು ಅನಿಯಮಿತವಾಗಿರುತ್ತದೆ ಮತ್ತು ಸ್ಥಾನದ ಅಸ್ತವ್ಯಸ್ತವಾದ ವಿನಿಮಯವಿದೆ. ಪ್ರತ್ಯೇಕ ಕಣಗಳು ಏರಿಳಿತದ ಟ್ರಾನ್ಸ್. ಪದ್ಯ ವೇಗಗಳಿಗೆ ಒಳಪಟ್ಟಿರುತ್ತವೆ, ಇದರಿಂದಾಗಿ ಚಲನೆಯು ರೆಕ್ಟಿಲಿನಿಯರ್ ಆಗಿರದೆ ಸುಳಿದಾಡುವ ಮತ್ತು ಸೈನಸ್ ಆಗಿರುತ್ತದೆ. ಒಂದು ನಿರ್ದಿಷ್ಟ ಹಂತದಲ್ಲಿ ಬಣ್ಣವನ್ನು ಚುಕ್ಕೆ ಹಾಕಿದರೆ, ಅದು ಹರಿವಿನ ಹರಿವಿನ ಉದ್ದಕ್ಕೂ ವೇಗವಾಗಿ ಹರಡುತ್ತದೆ. ಉದಾಹರಣೆಗೆ, ಪೈಪ್ನಲ್ಲಿ ಪ್ರಕ್ಷುಬ್ಧ ಹರಿವಿನ ಸಂದರ್ಭದಲ್ಲಿ, ಒಂದು ವಿಭಾಗದಲ್ಲಿ ವೇಗದ ತತ್ಕ್ಷಣದ ರೆಕಾರ್ಡಿಂಗ್ ಚಿತ್ರ 1(ಎ) ನಲ್ಲಿ ತೋರಿಸಿರುವಂತೆ ಅಂದಾಜು ವಿತರಣೆಯನ್ನು ಬಹಿರಂಗಪಡಿಸುತ್ತದೆ. ಸಾಮಾನ್ಯ ಅಳತೆ ಉಪಕರಣಗಳಿಂದ ದಾಖಲಿಸಲ್ಪಡುವ ಸ್ಥಿರ ವೇಗವನ್ನು ಚುಕ್ಕೆಗಳ ರೂಪರೇಖೆಯಲ್ಲಿ ಸೂಚಿಸಲಾಗುತ್ತದೆ, ಮತ್ತು ಪ್ರಕ್ಷುಬ್ಧ ಹರಿವು ತಾತ್ಕಾಲಿಕ ಸ್ಥಿರ ಸರಾಸರಿಯ ಮೇಲೆ ಅತಿಕ್ರಮಿಸಲಾದ ಅಸ್ಥಿರ ಏರಿಳಿತದ ವೇಗದಿಂದ ನಿರೂಪಿಸಲ್ಪಟ್ಟಿದೆ ಎಂಬುದು ಸ್ಪಷ್ಟವಾಗುತ್ತದೆ.
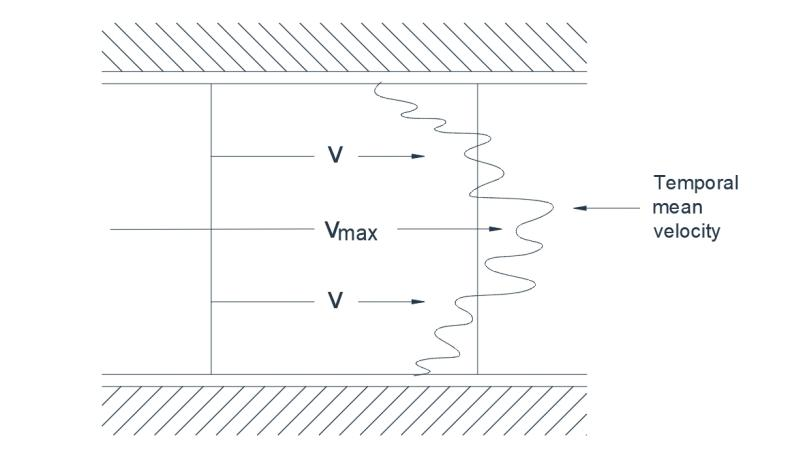
ಚಿತ್ರ 1(ಎ) ಪ್ರಕ್ಷುಬ್ಧ ಹರಿವು
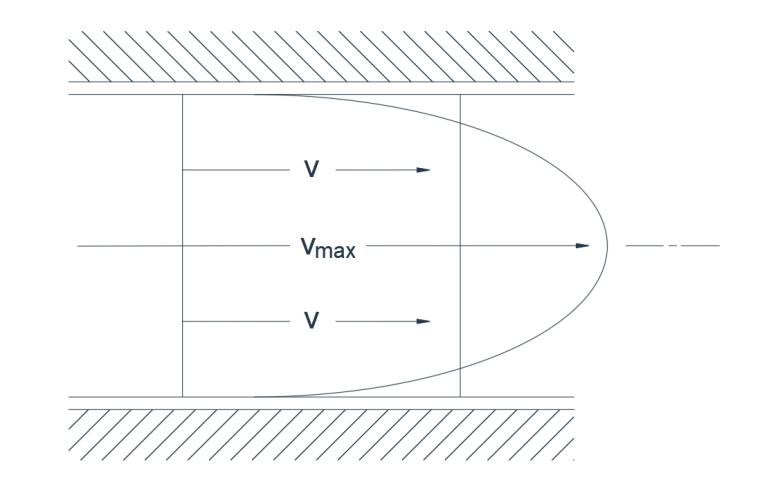
ಚಿತ್ರ 1(b) ಲ್ಯಾಮಿನಾರ್ ಹರಿವು
ಲ್ಯಾಮಿನಾರ್ ಹರಿವಿನಲ್ಲಿ ಎಲ್ಲಾ ದ್ರವ ಕಣಗಳು ಸಮಾನಾಂತರ ಮಾರ್ಗಗಳಲ್ಲಿ ಸಾಗುತ್ತವೆ ಮತ್ತು ವೇಗದ ಯಾವುದೇ ಅಡ್ಡ ಅಂಶವಿರುವುದಿಲ್ಲ. ಕ್ರಮಬದ್ಧವಾದ ಪ್ರಗತಿಯು ಪ್ರತಿ ಕಣವು ಯಾವುದೇ ವಿಚಲನವಿಲ್ಲದೆ ಅದರ ಹಿಂದಿನ ಕಣದ ಮಾರ್ಗವನ್ನು ನಿಖರವಾಗಿ ಅನುಸರಿಸುತ್ತದೆ. ಹೀಗಾಗಿ ತೆಳುವಾದ ವರ್ಣ ತಂತು ಪ್ರಸರಣವಿಲ್ಲದೆ ಹಾಗೆಯೇ ಉಳಿಯುತ್ತದೆ. ಲ್ಯಾಮಿನಾರ್ ಹರಿವಿನಲ್ಲಿ (ಚಿತ್ರ 1b) ಪ್ರಕ್ಷುಬ್ಧ ಹರಿವಿಗಿಂತ ಹೆಚ್ಚಿನ ಅಡ್ಡ ವೇಗದ ಗ್ರೇಡಿಯಂಟ್ ಇರುತ್ತದೆ. ಉದಾಹರಣೆಗೆ, ಪೈಪ್ಗೆ, ಸರಾಸರಿ ವೇಗ V ಮತ್ತು ಗರಿಷ್ಠ ವೇಗ V ಗರಿಷ್ಠ ಅನುಪಾತವು ಪ್ರಕ್ಷುಬ್ಧ ಹರಿವಿನಲ್ಲಿ 0,5 ಮತ್ತು ಲ್ಯಾಮಿನಾರ್ ಹರಿವಿನಲ್ಲಿ 0,05 ಆಗಿದೆ.
ಲ್ಯಾಮಿನಾರ್ ಹರಿವು ಕಡಿಮೆ ವೇಗಗಳು ಮತ್ತು ಸ್ನಿಗ್ಧತೆಯ ನಿಧಾನಗತಿಯ ದ್ರವಗಳೊಂದಿಗೆ ಸಂಬಂಧಿಸಿದೆ. ಪೈಪ್ಲೈನ್ ಮತ್ತು ಮುಕ್ತ-ಚಾನೆಲ್ ಹೈಡ್ರಾಲಿಕ್ಸ್ನಲ್ಲಿ, ವೇಗಗಳು ಯಾವಾಗಲೂ ಪ್ರಕ್ಷುಬ್ಧ ಹರಿವನ್ನು ಖಚಿತಪಡಿಸಿಕೊಳ್ಳಲು ಸಾಕಷ್ಟು ಹೆಚ್ಚಿರುತ್ತವೆ, ಆದರೂ ತೆಳುವಾದ ಲ್ಯಾಮಿನಾರ್ ಪದರವು ಘನ ಗಡಿಯ ಸಮೀಪದಲ್ಲಿ ಮುಂದುವರಿಯುತ್ತದೆ. ಲ್ಯಾಮಿನಾರ್ ಹರಿವಿನ ನಿಯಮಗಳನ್ನು ಸಂಪೂರ್ಣವಾಗಿ ಅರ್ಥಮಾಡಿಕೊಳ್ಳಲಾಗಿದೆ ಮತ್ತು ಸರಳ ಗಡಿ ಪರಿಸ್ಥಿತಿಗಳಿಗೆ ವೇಗ ವಿತರಣೆಯನ್ನು ಗಣಿತದ ಪ್ರಕಾರ ವಿಶ್ಲೇಷಿಸಬಹುದು. ಅದರ ಅನಿಯಮಿತ ಸ್ಪಂದನ ಸ್ವಭಾವದಿಂದಾಗಿ, ಪ್ರಕ್ಷುಬ್ಧ ಹರಿವು ಕಠಿಣ ಗಣಿತ ಚಿಕಿತ್ಸೆಯನ್ನು ಧಿಕ್ಕರಿಸಿದೆ ಮತ್ತು ಪ್ರಾಯೋಗಿಕ ಸಮಸ್ಯೆಗಳ ಪರಿಹಾರಕ್ಕಾಗಿ, ಪ್ರಾಯೋಗಿಕ ಅಥವಾ ಅರೆ-ಅನುಭವ ಸಂಬಂಧಗಳನ್ನು ಹೆಚ್ಚಾಗಿ ಅವಲಂಬಿಸುವುದು ಅವಶ್ಯಕ.

ಮಾದರಿ ಸಂಖ್ಯೆ: XBC-VTP
XBC-VTP ಸರಣಿಯ ಲಂಬವಾದ ಲಾಂಗ್ ಶಾಫ್ಟ್ ಅಗ್ನಿಶಾಮಕ ಪಂಪ್ಗಳು ಇತ್ತೀಚಿನ ರಾಷ್ಟ್ರೀಯ ಮಾನದಂಡ GB6245-2006 ಗೆ ಅನುಗುಣವಾಗಿ ತಯಾರಿಸಲಾದ ಏಕ ಹಂತದ, ಬಹು ಹಂತದ ಡಿಫ್ಯೂಸರ್ ಪಂಪ್ಗಳ ಸರಣಿಯಾಗಿದೆ. ಯುನೈಟೆಡ್ ಸ್ಟೇಟ್ಸ್ ಅಗ್ನಿಶಾಮಕ ರಕ್ಷಣಾ ಸಂಘದ ಮಾನದಂಡದ ಉಲ್ಲೇಖದೊಂದಿಗೆ ನಾವು ವಿನ್ಯಾಸವನ್ನು ಸುಧಾರಿಸಿದ್ದೇವೆ. ಇದನ್ನು ಮುಖ್ಯವಾಗಿ ಪೆಟ್ರೋಕೆಮಿಕಲ್, ನೈಸರ್ಗಿಕ ಅನಿಲ, ವಿದ್ಯುತ್ ಸ್ಥಾವರ, ಹತ್ತಿ ಜವಳಿ, ವಾರ್ಫ್, ವಾಯುಯಾನ, ಗೋದಾಮು, ಎತ್ತರದ ಕಟ್ಟಡ ಮತ್ತು ಇತರ ಕೈಗಾರಿಕೆಗಳಲ್ಲಿ ಬೆಂಕಿ ನೀರು ಸರಬರಾಜಿಗೆ ಬಳಸಲಾಗುತ್ತದೆ. ಇದು ಹಡಗು, ಸಮುದ್ರ ಟ್ಯಾಂಕ್, ಅಗ್ನಿಶಾಮಕ ಹಡಗು ಮತ್ತು ಇತರ ಪೂರೈಕೆ ಸಂದರ್ಭಗಳಿಗೂ ಅನ್ವಯಿಸಬಹುದು.
ತಿರುಗುವ ಮತ್ತು ಕಿರಿಕಿರಿಯುಂಟುಮಾಡುವ ಹರಿವು.
ಪ್ರತಿಯೊಂದು ದ್ರವ ಕಣವು ತನ್ನದೇ ಆದ ದ್ರವ್ಯರಾಶಿ ಕೇಂದ್ರದ ಬಗ್ಗೆ ಕೋನೀಯ ವೇಗವನ್ನು ಹೊಂದಿದ್ದರೆ ಆ ಹರಿವನ್ನು ತಿರುಗುವ ಹರಿವು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.
ಚಿತ್ರ 2a ನೇರ ಗಡಿಯನ್ನು ದಾಟಿ ಪ್ರಕ್ಷುಬ್ಧ ಹರಿವಿನೊಂದಿಗೆ ಸಂಬಂಧಿಸಿದ ವಿಶಿಷ್ಟ ವೇಗ ವಿತರಣೆಯನ್ನು ತೋರಿಸುತ್ತದೆ. ಏಕರೂಪವಲ್ಲದ ವೇಗ ವಿತರಣೆಯಿಂದಾಗಿ, ಮೂಲತಃ ಲಂಬವಾಗಿರುವ ಎರಡು ಅಕ್ಷಗಳನ್ನು ಹೊಂದಿರುವ ಕಣವು ಸಣ್ಣ ಪ್ರಮಾಣದ ತಿರುಗುವಿಕೆಯೊಂದಿಗೆ ವಿರೂಪಗೊಳ್ಳುತ್ತದೆ. ಚಿತ್ರ 2a ನಲ್ಲಿ, ವೃತ್ತಾಕಾರದಲ್ಲಿ ಹರಿಯುವುದು
ಪಥವನ್ನು ಚಿತ್ರಿಸಲಾಗಿದೆ, ವೇಗವು ತ್ರಿಜ್ಯಕ್ಕೆ ನೇರವಾಗಿ ಅನುಪಾತದಲ್ಲಿರುತ್ತದೆ. ಕಣದ ಎರಡು ಅಕ್ಷಗಳು ಒಂದೇ ದಿಕ್ಕಿನಲ್ಲಿ ತಿರುಗುತ್ತವೆ, ಇದರಿಂದಾಗಿ ಹರಿವು ಮತ್ತೆ ತಿರುಗುತ್ತದೆ.
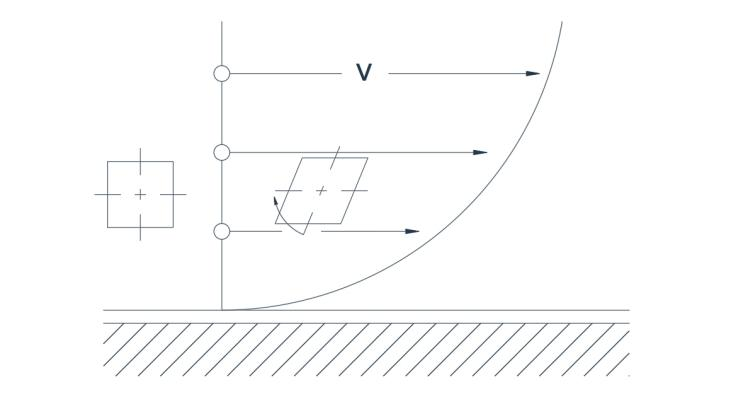
ಚಿತ್ರ 2 (ಎ) ತಿರುಗುವಿಕೆಯ ಹರಿವು
ಹರಿವು ಅಕ್ಷೀಯವಾಗಿರಬೇಕಾದರೆ, ನೇರ ಗಡಿಯ ಪಕ್ಕದಲ್ಲಿರುವ ವೇಗ ವಿತರಣೆಯು ಏಕರೂಪವಾಗಿರಬೇಕು (ಚಿತ್ರ 2 ಬಿ). ವೃತ್ತಾಕಾರದ ಮಾರ್ಗದಲ್ಲಿ ಹರಿವಿನ ಸಂದರ್ಭದಲ್ಲಿ, ವೇಗವು ತ್ರಿಜ್ಯಕ್ಕೆ ವಿಲೋಮ ಅನುಪಾತದಲ್ಲಿದ್ದರೆ ಮಾತ್ರ ಅಕ್ಷೀಯ ಹರಿವು ಅನ್ವಯಿಸುತ್ತದೆ ಎಂದು ತೋರಿಸಬಹುದು. ಚಿತ್ರ 3 ರಲ್ಲಿ ಮೊದಲ ನೋಟದಿಂದ, ಇದು ತಪ್ಪಾಗಿ ಕಾಣುತ್ತದೆ, ಆದರೆ ಹತ್ತಿರದಿಂದ ಪರಿಶೀಲಿಸಿದಾಗ ಎರಡು ಅಕ್ಷಗಳು ವಿರುದ್ಧ ದಿಕ್ಕಿನಲ್ಲಿ ತಿರುಗುತ್ತವೆ ಎಂದು ತಿಳಿದುಬಂದಿದೆ, ಇದರಿಂದಾಗಿ ಆರಂಭಿಕ ಸ್ಥಿತಿಯಿಂದ ಬದಲಾಗದ ಅಕ್ಷಗಳ ಸರಾಸರಿ ದೃಷ್ಟಿಕೋನವನ್ನು ಉತ್ಪಾದಿಸುವ ಸರಿದೂಗಿಸುವ ಪರಿಣಾಮವಿರುತ್ತದೆ.
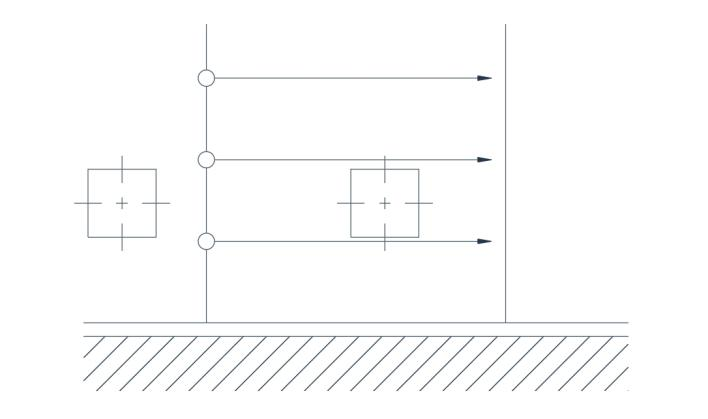
ಚಿತ್ರ 2(b) ಅಚಲ ಹರಿವು
ಎಲ್ಲಾ ದ್ರವಗಳು ಸ್ನಿಗ್ಧತೆಯನ್ನು ಹೊಂದಿರುವುದರಿಂದ, ನಿಜವಾದ ದ್ರವದ ಕಡಿಮೆ ಮಟ್ಟವು ಎಂದಿಗೂ ನಿಜವಾಗಿಯೂ ಕೆರಳಿಕೆಯಾಗುವುದಿಲ್ಲ ಮತ್ತು ಲ್ಯಾಮಿನಾರ್ ಹರಿವು ಸಹಜವಾಗಿ ಹೆಚ್ಚು ತಿರುಗುವಿಕೆಯಿಂದ ಕೂಡಿರುತ್ತದೆ. ಹೀಗಾಗಿ ಕೆರಳಿಕೆ ಹರಿವು ಒಂದು ಕಾಲ್ಪನಿಕ ಸ್ಥಿತಿಯಾಗಿದ್ದು, ಇದು ಶೈಕ್ಷಣಿಕ ಆಸಕ್ತಿಯನ್ನು ಹೊಂದಿರುತ್ತದೆ - ಪ್ರಕ್ಷುಬ್ಧ ಹರಿವಿನ ಅನೇಕ ಸಂದರ್ಭಗಳಲ್ಲಿ ತಿರುಗುವಿಕೆಯ ಗುಣಲಕ್ಷಣಗಳು ತುಂಬಾ ಅತ್ಯಲ್ಪವಾಗಿದ್ದು ಅವುಗಳನ್ನು ನಿರ್ಲಕ್ಷಿಸಬಹುದು ಎಂಬ ಅಂಶವಿಲ್ಲದಿದ್ದರೆ ಮಾತ್ರ. ಇದು ಅನುಕೂಲಕರವಾಗಿದೆ ಏಕೆಂದರೆ ಹಿಂದೆ ಉಲ್ಲೇಖಿಸಲಾದ ಶಾಸ್ತ್ರೀಯ ಹೈಡ್ರೊಡೈನಾಮಿಕ್ಸ್ನ ಗಣಿತದ ಪರಿಕಲ್ಪನೆಗಳ ಮೂಲಕ ಕೆರಳಿಕೆ ಹರಿವನ್ನು ವಿಶ್ಲೇಷಿಸಲು ಸಾಧ್ಯವಿದೆ.
ಕೇಂದ್ರಾಪಗಾಮಿ ಸಮುದ್ರ ನೀರಿನ ಗಮ್ಯಸ್ಥಾನ ಪಂಪ್
ಮಾದರಿ ಸಂಖ್ಯೆ: ASN ASNV
ಮಾದರಿ ASN ಮತ್ತು ASNV ಪಂಪ್ಗಳು ಏಕ-ಹಂತದ ಡಬಲ್ ಸಕ್ಷನ್ ಸ್ಪ್ಲಿಟ್ ವಾಲ್ಯೂಟ್ ಕೇಸಿಂಗ್ ಕೇಂದ್ರಾಪಗಾಮಿ ಪಂಪ್ಗಳು ಮತ್ತು ನೀರಿನ ಕೆಲಸಗಳು, ಹವಾನಿಯಂತ್ರಣ ಪರಿಚಲನೆ, ಕಟ್ಟಡ, ನೀರಾವರಿ, ಒಳಚರಂಡಿ ಪಂಪ್ ಸ್ಟೇಷನ್, ವಿದ್ಯುತ್ ಶಕ್ತಿ ಕೇಂದ್ರ, ಕೈಗಾರಿಕಾ ನೀರು ಸರಬರಾಜು ವ್ಯವಸ್ಥೆ, ಅಗ್ನಿಶಾಮಕ ವ್ಯವಸ್ಥೆ, ಹಡಗು, ಕಟ್ಟಡ ಮತ್ತು ಮುಂತಾದವುಗಳಿಗೆ ಬಳಸಿದ ಅಥವಾ ದ್ರವ ಸಾಗಣೆಯಾಗಿದೆ.

ಸ್ಥಿರ ಮತ್ತು ಅಸ್ಥಿರ ಹರಿವು.
ಯಾವುದೇ ಹಂತದಲ್ಲಿ ಪರಿಸ್ಥಿತಿಗಳು ಸಮಯಕ್ಕೆ ಅನುಗುಣವಾಗಿ ಸ್ಥಿರವಾಗಿದ್ದರೆ ಹರಿವು ಸ್ಥಿರವಾಗಿರುತ್ತದೆ ಎಂದು ಹೇಳಲಾಗುತ್ತದೆ. ಈ ವ್ಯಾಖ್ಯಾನದ ಕಟ್ಟುನಿಟ್ಟಾದ ವ್ಯಾಖ್ಯಾನವು ಪ್ರಕ್ಷುಬ್ಧ ಹರಿವು ಎಂದಿಗೂ ನಿಜವಾಗಿಯೂ ಸ್ಥಿರವಾಗಿಲ್ಲ ಎಂಬ ತೀರ್ಮಾನಕ್ಕೆ ಕಾರಣವಾಗುತ್ತದೆ. ಆದಾಗ್ಯೂ, ಪ್ರಸ್ತುತ ಉದ್ದೇಶಕ್ಕಾಗಿ ಸಾಮಾನ್ಯ ದ್ರವ ಚಲನೆಯನ್ನು ಮಾನದಂಡವಾಗಿ ಮತ್ತು ಪ್ರಕ್ಷುಬ್ಧತೆಗೆ ಸಂಬಂಧಿಸಿದ ಅನಿಯಮಿತ ಏರಿಳಿತಗಳನ್ನು ದ್ವಿತೀಯಕ ಪ್ರಭಾವವಾಗಿ ಪರಿಗಣಿಸುವುದು ಅನುಕೂಲಕರವಾಗಿದೆ. ಸ್ಥಿರ ಹರಿವಿನ ಸ್ಪಷ್ಟ ಉದಾಹರಣೆಯೆಂದರೆ ವಾಹಕ ಅಥವಾ ತೆರೆದ ಚಾನಲ್ನಲ್ಲಿ ಸ್ಥಿರವಾದ ವಿಸರ್ಜನೆ.
ಪರಿಣಾಮವಾಗಿ, ಸಮಯಕ್ಕೆ ಸಂಬಂಧಿಸಿದಂತೆ ಪರಿಸ್ಥಿತಿಗಳು ಬದಲಾಗುವಾಗ ಹರಿವು ಅಸ್ಥಿರವಾಗಿರುತ್ತದೆ. ಅಸ್ಥಿರ ಹರಿವಿನ ಉದಾಹರಣೆಯೆಂದರೆ ನಾಲೆ ಅಥವಾ ತೆರೆದ ಚಾನಲ್ನಲ್ಲಿ ಬದಲಾಗುವ ವಿಸರ್ಜನೆ; ಇದು ಸಾಮಾನ್ಯವಾಗಿ ಸ್ಥಿರ ವಿಸರ್ಜನೆಗೆ ಅನುಕ್ರಮವಾಗಿ ಅಥವಾ ನಂತರ ಬರುವ ಅಸ್ಥಿರ ವಿದ್ಯಮಾನವಾಗಿದೆ. ಇತರ ಪರಿಚಿತ
ಹೆಚ್ಚು ಆವರ್ತಕ ಸ್ವಭಾವದ ಉದಾಹರಣೆಗಳೆಂದರೆ ತರಂಗ ಚಲನೆ ಮತ್ತು ಉಬ್ಬರವಿಳಿತದ ಹರಿವಿನಲ್ಲಿ ದೊಡ್ಡ ನೀರಿನ ಕಾಯಗಳ ಚಕ್ರೀಯ ಚಲನೆ.
ಹೈಡ್ರಾಲಿಕ್ ಎಂಜಿನಿಯರಿಂಗ್ನಲ್ಲಿನ ಹೆಚ್ಚಿನ ಪ್ರಾಯೋಗಿಕ ಸಮಸ್ಯೆಗಳು ಸ್ಥಿರ ಹರಿವಿಗೆ ಸಂಬಂಧಿಸಿವೆ. ಇದು ಅದೃಷ್ಟ, ಏಕೆಂದರೆ ಅಸ್ಥಿರ ಹರಿವಿನಲ್ಲಿನ ಸಮಯದ ವ್ಯತ್ಯಾಸವು ವಿಶ್ಲೇಷಣೆಯನ್ನು ಗಣನೀಯವಾಗಿ ಸಂಕೀರ್ಣಗೊಳಿಸುತ್ತದೆ. ಅಂತೆಯೇ, ಈ ಅಧ್ಯಾಯದಲ್ಲಿ, ಅಸ್ಥಿರ ಹರಿವಿನ ಪರಿಗಣನೆಯು ಕೆಲವು ಸರಳ ಪ್ರಕರಣಗಳಿಗೆ ಸೀಮಿತವಾಗಿರುತ್ತದೆ. ಆದಾಗ್ಯೂ, ಸಾಪೇಕ್ಷ ಚಲನೆಯ ತತ್ವದ ಕಾರಣದಿಂದಾಗಿ ಅಸ್ಥಿರ ಹರಿವಿನ ಹಲವಾರು ಸಾಮಾನ್ಯ ನಿದರ್ಶನಗಳನ್ನು ಸ್ಥಿರ ಸ್ಥಿತಿಗೆ ಇಳಿಸಬಹುದು ಎಂಬುದನ್ನು ಮನಸ್ಸಿನಲ್ಲಿಟ್ಟುಕೊಳ್ಳುವುದು ಮುಖ್ಯ.
ಹೀಗಾಗಿ, ಸ್ಥಿರ ನೀರಿನ ಮೂಲಕ ಚಲಿಸುವ ಹಡಗನ್ನು ಒಳಗೊಂಡಿರುವ ಸಮಸ್ಯೆಯನ್ನು, ಆ ಹಡಗನ್ನು ಸ್ಥಿರವಾಗಿ ಮತ್ತು ನೀರು ಚಲನೆಯಲ್ಲಿರುವಂತೆ ಮರುರೂಪಿಸಬಹುದು; ದ್ರವದ ವರ್ತನೆಯ ಹೋಲಿಕೆಗೆ ಏಕೈಕ ಮಾನದಂಡವೆಂದರೆ ಸಾಪೇಕ್ಷ ವೇಗವು ಒಂದೇ ಆಗಿರಬೇಕು. ಮತ್ತೊಮ್ಮೆ, ಆಳವಾದ ನೀರಿನಲ್ಲಿ ತರಂಗ ಚಲನೆಯನ್ನು ಕಡಿಮೆ ಮಾಡಬಹುದು
ಒಬ್ಬ ವೀಕ್ಷಕನು ಅಲೆಗಳೊಂದಿಗೆ ಒಂದೇ ವೇಗದಲ್ಲಿ ಚಲಿಸುತ್ತಾನೆ ಎಂದು ಊಹಿಸುವ ಮೂಲಕ ಸ್ಥಿರ ಸ್ಥಿತಿಯನ್ನು ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ.

ಡೀಸೆಲ್ ಎಂಜಿನ್ ಲಂಬ ಟರ್ಬೈನ್ ಮಲ್ಟಿಸ್ಟೇಜ್ ಸೆಂಟ್ರಿಫ್ಯೂಗಲ್ ಇನ್ಲೈನ್ ಶಾಫ್ಟ್ ವಾಟರ್ ಡ್ರೈನೇಜ್ ಪಂಪ್ ಈ ರೀತಿಯ ಲಂಬ ಒಳಚರಂಡಿ ಪಂಪ್ ಅನ್ನು ಮುಖ್ಯವಾಗಿ ಸವೆತವಿಲ್ಲದೆ, 60 °C ಗಿಂತ ಕಡಿಮೆ ತಾಪಮಾನದಲ್ಲಿ, ಅಮಾನತುಗೊಂಡ ಘನವಸ್ತುಗಳನ್ನು (ಫೈಬರ್, ಗ್ರಿಟ್ಗಳನ್ನು ಒಳಗೊಂಡಿಲ್ಲ) 150 mg/L ಗಿಂತ ಕಡಿಮೆ ಒಳಚರಂಡಿ ಅಥವಾ ತ್ಯಾಜ್ಯ ನೀರನ್ನು ಪಂಪ್ ಮಾಡಲು ಬಳಸಲಾಗುತ್ತದೆ. VTP ಪ್ರಕಾರದ ಲಂಬ ಒಳಚರಂಡಿ ಪಂಪ್ VTP ಪ್ರಕಾರದ ಲಂಬ ನೀರಿನ ಪಂಪ್ಗಳಲ್ಲಿದೆ, ಮತ್ತು ಹೆಚ್ಚಳ ಮತ್ತು ಕಾಲರ್ ಆಧಾರದ ಮೇಲೆ, ಟ್ಯೂಬ್ ಎಣ್ಣೆ ನಯಗೊಳಿಸುವಿಕೆಯನ್ನು ನೀರು ಎಂದು ಹೊಂದಿಸಿ. 60 °C ಗಿಂತ ಕಡಿಮೆ ತಾಪಮಾನದಲ್ಲಿ ಹೊಗೆಯಾಡಿಸಬಹುದು, ಒಳಚರಂಡಿ ಅಥವಾ ತ್ಯಾಜ್ಯ ನೀರಿನ ನಿರ್ದಿಷ್ಟ ಘನ ಧಾನ್ಯವನ್ನು (ಕಬ್ಬಿಣ ಮತ್ತು ಸೂಕ್ಷ್ಮ ಮರಳು, ಕಲ್ಲಿದ್ದಲು, ಇತ್ಯಾದಿ) ಹೊಂದಲು ಕಳುಹಿಸಬಹುದು.
ಏಕರೂಪ ಮತ್ತು ಏಕರೂಪವಲ್ಲದ ಹರಿವು.
ಹರಿವಿನ ಹಾದಿಯಲ್ಲಿ ಒಂದು ಬಿಂದುವಿನಿಂದ ಇನ್ನೊಂದು ಬಿಂದುವಿಗೆ ವೇಗ ವೆಕ್ಟರ್ನ ಪ್ರಮಾಣ ಮತ್ತು ದಿಕ್ಕಿನಲ್ಲಿ ಯಾವುದೇ ವ್ಯತ್ಯಾಸವಿಲ್ಲದಿದ್ದಾಗ ಹರಿವನ್ನು ಏಕರೂಪವೆಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಈ ವ್ಯಾಖ್ಯಾನದ ಅನುಸರಣೆಗಾಗಿ, ಪ್ರತಿ ಅಡ್ಡ-ವಿಭಾಗದಲ್ಲಿ ಹರಿವಿನ ವಿಸ್ತೀರ್ಣ ಮತ್ತು ವೇಗ ಎರಡೂ ಒಂದೇ ಆಗಿರಬೇಕು. ವೇಗ ವೆಕ್ಟರ್ ಸ್ಥಳದೊಂದಿಗೆ ಬದಲಾಗಿದಾಗ ಏಕರೂಪವಲ್ಲದ ಹರಿವು ಸಂಭವಿಸುತ್ತದೆ, ಒಂದು ವಿಶಿಷ್ಟ ಉದಾಹರಣೆಯೆಂದರೆ ಒಮ್ಮುಖವಾಗುವ ಅಥವಾ ಬೇರೆಡೆಗೆ ಹೋಗುವ ಗಡಿಗಳ ನಡುವಿನ ಹರಿವು.
ಈ ಎರಡೂ ಪರ್ಯಾಯ ಹರಿವಿನ ಪರಿಸ್ಥಿತಿಗಳು ಮುಕ್ತ-ಚಾನೆಲ್ ಹೈಡ್ರಾಲಿಕ್ಸ್ನಲ್ಲಿ ಸಾಮಾನ್ಯವಾಗಿದೆ, ಆದಾಗ್ಯೂ ಕಟ್ಟುನಿಟ್ಟಾಗಿ ಹೇಳುವುದಾದರೆ, ಏಕರೂಪದ ಹರಿವನ್ನು ಯಾವಾಗಲೂ ಲಕ್ಷಣರಹಿತವಾಗಿ ಸಮೀಪಿಸುವುದರಿಂದ, ಇದು ಒಂದು ಆದರ್ಶ ಸ್ಥಿತಿಯಾಗಿದ್ದು, ಅದನ್ನು ಅಂದಾಜು ಮಾಡಲಾಗುತ್ತದೆ ಮತ್ತು ಎಂದಿಗೂ ವಾಸ್ತವವಾಗಿ ಸಾಧಿಸಲಾಗುವುದಿಲ್ಲ. ಪರಿಸ್ಥಿತಿಗಳು ಸಮಯಕ್ಕಿಂತ ಜಾಗಕ್ಕೆ ಸಂಬಂಧಿಸಿವೆ ಮತ್ತು ಆದ್ದರಿಂದ ಮುಚ್ಚಿದ ಹರಿವಿನ ಸಂದರ್ಭಗಳಲ್ಲಿ (ಉದಾ. ಒತ್ತಡದಲ್ಲಿರುವ ಕೊಳವೆಗಳು), ಅವು ಹರಿವಿನ ಸ್ಥಿರ ಅಥವಾ ಅಸ್ಥಿರ ಸ್ವಭಾವದಿಂದ ಸಾಕಷ್ಟು ಸ್ವತಂತ್ರವಾಗಿರುತ್ತವೆ ಎಂಬುದನ್ನು ಗಮನಿಸಬೇಕು.
ಪೋಸ್ಟ್ ಸಮಯ: ಮಾರ್ಚ್-29-2024
 sales@tkflow.com
sales@tkflow.com 
